diesem liegt ein irrationales Verhältnis zugrunde. Die Prozentangaben bei Wikipedia lassen dies nicht vermuten und sind auch wenig hilfreich. Wir wissen, daß Euklid bereits um 300 b.c. sich diesem Zahlenverhältnis widmete.
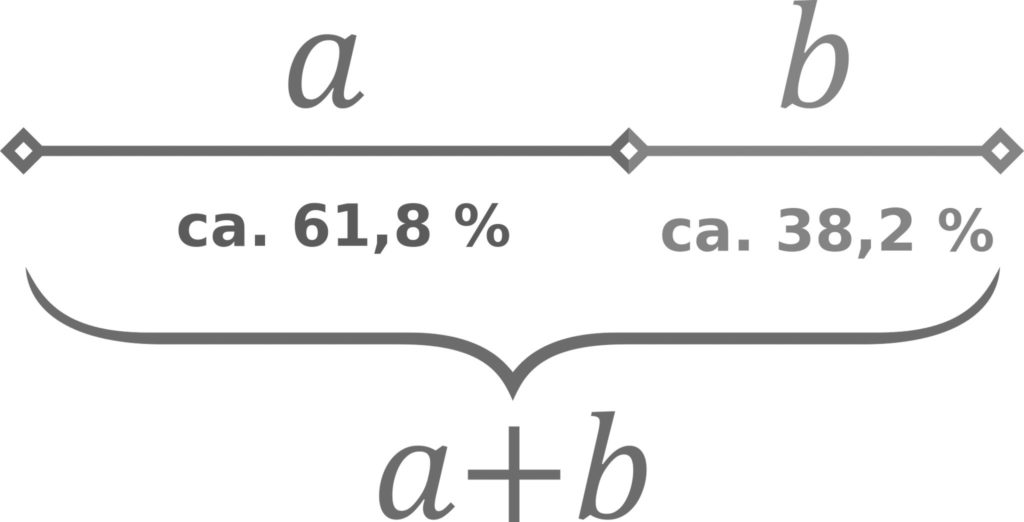
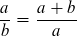
Es existieren zahlreiche algebraische und geometrische Verfahren dieses Verhältnis in eine konkrete Lösung zu überführen. Wie kommt es zu diesem Verhältnis, welche Überlegungen liegen diesem zugrunde und gibt es einen empirischen oder anderen Zusammenhang, der diesem Verhältnis eine ästhetische Bedeutung zumisst, e.g. aus der experimentellen Ästhetik*.
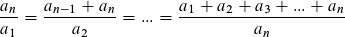
Nehmen wir den Quotienten zweier benachbarter Glieder der Fibonacci**-Folge und bilden den Grenzwert dieser neuen Folge, dann konvergiert dieser gegen τ, die Goldene Schnittzahl. Deren Quadrat und Kehrwert haben dieselben Dezimalstellen :
,6180339 …
Da liegt ganz offenbar etwas Magie inne, in dieser Zahl, in diesem Verhältnis. Können wir mit zwei Zahlen, die z.B für Strecken stehen, noch weitere Verhältnisse definieren, die uns ebenso frei halten von absoluten Werten und mit einer Einschränkung wie a > b versehen sind und reelle, nicht negative Lösungen haben. Wenn wir von Zahlenverhältnissen sprechen, meinen wir Proportionen, wir beziehen die beiden Zahlen a und b aufeinander. Dies leistet der Quotient der beiden Zahlen. Also sei a / b = q, mit q > 1 und wir nennen dieses Verhältnis Fundamentalproportion. Diese können wir z.B. einer Konstanten gleichsetzen, was wir außer Betracht lassen, oder einer aus den beiden Größen abgeleiteten Bedingung. Wählen wir diese Bedingung in einer kanonischen Form, haben wir folgende Möglichkeiten : Summe, Differenz, Quotient, Produkt, wobei wir Vielfache, nicht-positive, triviale ( z.B. a = b2 ), q < 1 als nicht-kanonisch klassifizieren, wie z.B. 3*a / b.
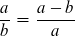
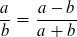
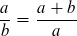
Die Diskriminante, die wir für obige Gleichung 1. erhalten, zeigt uns, daß hier keine reelle Lösung existiert, zudem ist q < 1. Gleichung 2. hat eine komplexe Lösung und q ist < 1. Eine „kanonische“ Bedingung ist also nur die ursprüngliche, obige Definition, sie ergibt sich zwangsläufig aus den einfachen Prämissen und ihre Lösung ergibt
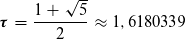
”Daß zwei Dinge sich auf eine schöne Art vereinigen ohne ein drittes, ist unmöglich. Denn es muss ein Band zwischen ihnen entstehen, das sie vereinigt. Das kann die Proportion am besten vollbringen. Denn wenn von irgend drei Zahlen die mittlere sich zu der kleinsten verhält, wie die größte zu der mittleren selbst und umgekehrt, die kleinste zu dermittleren wie die mittlere zur größten, dann wird das Letzte und das Erste das Mittlere und das Mittlere Erstes und Letztes, alles wird also mit Notwendigkeit dasselbe, und da es dasselbe wird, bildet es ein Einziges.“
Platon: Timaios
*Visuelle Statik – II: Empirische Studien zum Problem von Last und Stütze
Christoph Piesbergen, Kurt Müller & Wolfgang Tunner, Universität München
** Filius Bonacci



