Im Rahmen der tensoriell-differentialgeometrischen Aufstellung von nichtlinearen, abhängigen Differentialgleichungen der ART wird eine torsionsfreie Abbildung gefordert ( Levi-Civita-Zusammenhang ) :
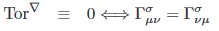
Das heißt, wenn die Torsion identisch Null ist, dann sind die Christoffelsymbole symmetrisch in den kovarianten Indizes.
Die Torsion ist mit dem Begriff des Nullteilers verbunden und ist vereinfacht gesprochen ein Maß für die Abweichung von der Injektivität einer Abbildung, zB. einer Gruppenverknüpfung in SL (n,K), einer Matrizenmultiplikation. Besteht jenseits des Formalismus zur Beschreibung der Teilchenspins eine geometrisch-physikalische Verwandtschaft hierzu.



