Die Mengen ℕ und ℝ sind im alltäglichen Gebrauch. Die darauf fussenden Körper verursachen dabei kaum eine Nachdenklichkeit. Abzählbar und Überabzählbar sind wesentliche Characteristika und somit Unterscheidungsmerkmale, Diskretheit und Kontinuum mit anderen Worten.
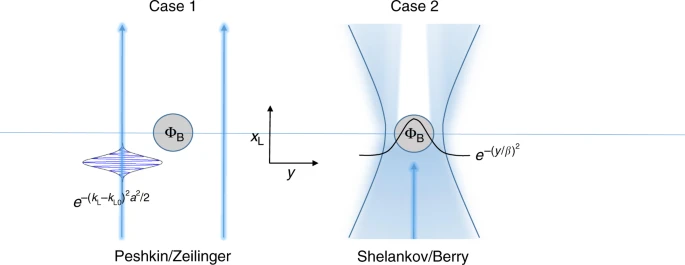
Die Mengen und ihre Eigenschaften korrespondieren mit den quanten-physikalischen Begriffen Teilchen und Welle. Orts- und Impulsraum sind sich jeweils Fouriertransformierte und veranschaulichen somit die Unschärferelation. Lokalität wird hergestellt durch den Teilchencharacter des Quantums (Kollaps der Wellenfunktion). Falls Bereiche bezüglich der lokalen Wechselwirkung nicht „einfach zusammenhängend“ sind, kann sich diese Topologie allerdings auf verschiedenen Quanteneigenschaften auswirken. Hier beobachten wir dann Interferenzen der Quanten, die entweder auf dispersiven Effekten oder Quantenkrafteffekte im feldfreien Raum fußen. In wieweit Vektor-Potentiale dadurch physikalische Realität gewinnen, ist ganz offenbar noch in der Diskussion und noch nicht entschieden. Gibt man das Prinzip Lokalität in seiner Unbedingtheit auf, treten noch andere Erklärungen auf die Weltbühne. Die Topologie, Struktur des Raumes bezüglich Gestalt und nichtlokaler Eigenschaften (s.o.) spielt bei Quantenprozessen wie Interferenz, also Phasenbezug, Dispersionsrelationen in verschiedene Raumrichtungen (transversal) u.a.m. eine wesentliche Rolle. Die Struktur des Raumes bedingt also Wechselwirkungsprozesse auf Quantenebene. Die Nähe dieser physikalischen Phänomene zum OSR ist damit offenbar.
*Ontic Structural Realism



