Bevor ich mich oberflächlich der gestellten Überschrift widme, möchte ich Marcel Großmann u.a. zitieren, ein enger Freund und Studienkollege von Einstein und das Mastermind bezüglich der Entwicklung von geeigneten mathematischen Werkzeugen zur Formulierung der ART*.
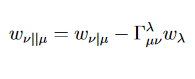
Theorie der Gravitation
Der mathematische Grundgedanke der Einstein’schen Gravita-
Mathematische Begriffsbildungen zur Gravitationstheorie, Marcel Grossmann, 1913
tionstheorie, ein Gravitationsfeld zu charakterisieren durch eine quadra-
tische Differentialform mit variabeln Koeffizienten, zwingt zu einer
Verallgemeinerung der Begriffsbildungen und Methoden der Vektor-
analysis.
It took eight years after Einstein announced the basic physical ideas behind the relativistic gravity theory before the proper mathematical formulation of general relativity was mastered.
Einstein and hilbert:The creation of general relativity, Ivan T. Todorov, Lecture @ International Centre for Theoretical Physics, Trieste, 9 December 1992
I. Begriff einer n fach ausgedehnten Grösse.
Ueber die Hypothesen, welche der Geometrie zu Grunde liegen. Bernhard Riemann, Abhandlungen der Königlichen Gesellschaft der Wissenschaften zu Göttingen, Band 13, S. 133-150, 1867, Habilitationsschrift
Indem ich nun von diesen Aufgaben zunächst die erste, die Entwicklung des Begriffs mehrfach ausgedehnter Grössen, zu lösen versuche, glaube ich um so mehr auf eine nachsichtige Beurtheilung Anspruch machen zu dürfen, da ich in dergleichen Arbeiten philosophischer Natur, wo die Schwierigkeiten mehr in den Begriffen, als in der Construction liegen, wenig geübt bin und ich ausser einigen ganz kurzen Andeutungen, welche Herr Geheimer Hofrath Gauss in der zweiten Abhandlung über die biquadratischen Reste, in den Göttingenschen gelehrten Anzeigen und in seiner Jubiläumsschrift darüber gegeben hat, und einigen philosophischen Untersuchungen Herbart’s, durchaus keine Vorarbeiten benutzen konnte.
Unser Anschaungsraum ist ein Konstrukt, eine komplexe Verquickung von Realitäten, Wirklichkeit und Vorstellungen. Er besteht aus Ansichten, Perspektiven und einer durch unseren Intellekt verliehenen, zusätzlichen Struktur. Unsere sinnliche Wahrnehmung und unser Intellekt navigieren uns durch diesen Raum. Er ähnelt dem euklidischen Raum, wir können diesen Begriff synonym verwenden, wenn wir subjektive Aspekte aus und vor lassen. Eine Wechselwirkung zwischen Ding und Raum, begründet durch dessen Einbettung in diesen Raum, ist alleinig schon dadurch gegeben, daß dieses durch seine Extensionailtät einen Ort ( Ereignis im Minkowski-Raum ) exklusiv belegt, auszeichnet (Fermi-Dirac-Spinstatistik). Ein analytische Annäherung an den Raumbegriff führt uns zu dessen mathematischer Definition : Menge + Struktur = Raum. Wenn wir den Euklidischen Raum und Raumbegriff (* ~300 v.C.) verlassen, folgen erst 1867 durch B. Riemann Überlegungen, diesen fundamental zu erweitern und zu verallgemeinern : die Mannigfaltigkeiten.
Einstein stand in einem regen Austausch mit Kollegen im Wissenschaftsbetrieb Anfang des letzten Jahrhunderts, wie Ernst Mach z.B. Ernst Mach stand dem Wiener Kreis nahe (Neopositivismus) und reflektierte mit Einstein mögliche Ursachen für das Äquivalenprinzip von schwerer und träger Masse. Im Gegensatz zu Mach glaubte Einstein nicht an den ursächlichen Einfluss entfernter kosmischer Massen in diesem Zusammenhang. Er vermutete eher einen wechselwirkenden (!) Zusammenhang zwischen Raum und den darin befindlichen Massen. Dieser Grundgedanke war es wohl, der zu einer allgemeinen Theorie der Gravitation führte.
Die Lösungen der ART* für „masselose Universen“ (flache Raumzeit), zeigen übrigens und beweisen Einsteins obige Auffassung, da Fliehkräfte für Probekörper darin existieren (s.a. newtonsches Gedankenexperiment : rotierender Eimer).
Zur Errichtung einer allgemeinen Theorie der Gravitation reichten die Eigenschaften des euklidischen Raumes nicht aus. Die Arbeiten von Riemann aber lieferten das Basismaterial, auf dem man aufbauen konnte : ein universeller Raum, mit geeigneter Struktur, inklusive Einbettungen, beliebig differenzierbar und mit diffeomorphen Abbildungen. Karten und Atlanten, Tangentialräume und deren Vereinigungen sorgen für punktuelle, euklidische Unterräume, deren Verbindung, mathematische Konnexion genannt, die Voraussetzung für mitwandernde Metriken auf beliebigen Wegen schuf. Die kovariante Formulierung der Theorie sorgte u.a. für deren Koordinatenunabhängkeit. Ein zentraler Bestandteil dieser mathematischen Form ist die kovariante Ableitung in und für die verwandten Tensoren, wie z.B. der Energie-Impuls-Tensor.
*Allgemeine Relativitätstheorie



